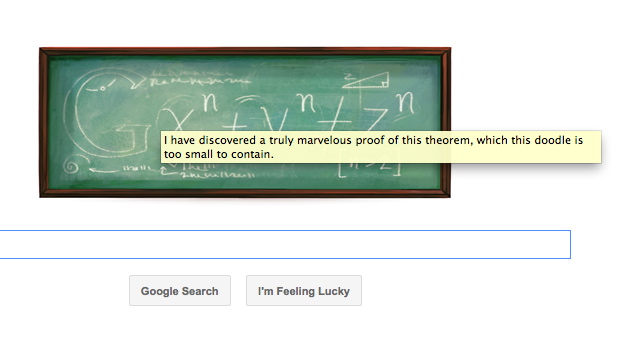
Google’s latest logo doodle celebrates the 410th anniversary of the birthday of French mathematician and lawyer Pierre de Fermat on August 17th with a chalkboard with mathematical equation, symbols, and an erased Google logo.
The California based company and search engine giant Google also nods playfully to the conditions of “Fermat’s Last Theorem,” (pictured on the Doodle’s chalkboard) — which the Frenchman so notably proposed about 1637 by scribbling in his copy of the ancient Greek text Arithmetica by Diophantus.
Google also embedded a hidden message in Fermat’s Doodle: “I have discovered a truly marvelous proof of this theorem, which this doodle is too small to contain.” Clicking the chalkboard image with initiate the search term “Pierre de Fermat.”
Fermat is an amateur mathematician who made contributions to analytic geometry, probability and optics, as well as his smallest ordinates discovery that is related to differential calculus.
Google Doodle today : Fermat and his Last Theorem
Fermat boasted by adding in Latin that he had no room to write his discovered proof for the theorem. Translation: “I have discovered a truly marvelous demonstration of this proposition that this margin is too narrow to contain.”
It would be more than 350 years — if our math is correct — until British mathematician Andrew Wiles, working alone in his attic for seven years, would find (in the mid-’90s) a proof for the world’s “most difficult math problem.”
Fermat is also recognized for his discovery of the smallest ordinates of curved lines, which is comparable to another branch of mathematics, the differential calculus. Apparently, Calculus is divided into two parts, the integral and the differential.
Thank you for confusing our little heads and happy birthday to this most amazing of a mathematicians Pierre de Fermat.
[adrotate group=”24″ banner=”27″]


FERMAT ‘s Last Theorem.
The conditions
X,Y,Z,N are the integers.>0 and N>2.
PROOF Z^N=/X^N+Y^N.
Suppose
Z^3=X^3+Y^3.
=>
Z=(X^3+Y^3)^1/3.
Define F(X,Y).
F(X,Y)= (X^3+Y^3)^1/3 – [(X-X-1)^3+(Y-X-1)^3]^1/3.
=>
F(X,Y)=Z- [(Y-X-1)^3-1]^1/3.
Because.
(Y-X-1) is an integer so
[(Y-X-1)^3-1]^1/3. and [(Y-X-1)^3-1]^2/3. are two irrational numbers.
=>
{ [(Y-X-1)^3-1]^1/3 – [ Z – F(X,Y)] }^3=0.
=>
[(Y-X-1)^3-1] +3[(Y-X-1)^3-1]^2/3*Z +V=0.
Because
3[(Y-X-1)^3-1]^2/3*Z is an irrational number So
V is an irrational number.
Because
3Z[(Y-X-1)^3-1]^2/3 = – {[(Y-X-1)^3-1] +.V}
So
an integer * an irrational number=an integer+an irrational number.
Unreasonable.
So
Z is an irrational number.
So
Z^3=/X^3+Y^3.
Similar.
Z^N=/X^N+Y^N.
ISHTAR.
Problem one.
3 cube+4 cube+5 cube=6 cube.
problem two.
1 cube….2 cube….3 cube….4 cube….5 cube….6cube..
1square….2 square….3 square….4 square….5 square….6 square….
We have new series with:1 cube-1 square….2 cube-2 square….3 cube-3 square….4 cube -4 square….
0….4….18….48….100….180….
We have new series with :4-0….18-4….48-18….100-48…..
4….14….30….52….
We have new series with 14-4….30-14….
10….16….22….
We have new series with:16-10….22-16….
6….6….
6=1 multiply 2 multiply 3=3!
6-6=0
problem three.
1 cube….2 cube….3 cube….4 cube….5 cube….6 cube….
We have new series with:2 cube-1 cube….3 cube-2 cube….4 cube-3 cube….5 cube-4 cube….
1….7….19….37….61….91….
We have new series with ;7-1….19-7….37-19….61-37….91-61….
6….12….18….24….30….
We have new series with :
12-6….18-12….24-18….30-24….
6….6….6….6
6= 1 multiply 2 multiply 3=3!
6-6=0.
Why both method have consequences same?
problem four.
1 exponent n+2 exponent n+3 exponent n+4 exponent n+……..+a exponent n+…….
I proved this formula with a and n are any number of sets of natural number.
problem five.
the series of natural number:123456789….
Make new series of number with:1+2….1+2+3….1+2+3+4….1+2+3+4+5….
1….3….6….10….15….
Make new series of number with:1+3….1+3+6….1+3+6+10….1+3+6+10+15….
1….4….10….20….35….Name this series is A.
for series of number1 square….2 square….3 square….4 square….
1….4…..9…..16…..25….
Make new series of number with:1-1….4-4….10-9….20-16….35-25….
0….0….1….4….10
Why it again series A?
problem six.
1 exponent n…. 2 exponent n….3 wxponent n….4 exponent n….
Make new series of number with:2 exponent n-1 exponent n….3 exponent n-2 exponent n….4 exponent n-3 exponent n….5 wexponent n-4 exponent n….
From this new series of number with method subtract same same .We have other series of number.
If continue to subtract the end is zero.Why?
prolem seven.
1+2+3+4+5+6+7.+……+n=S1
S2=1 square+2 square+3 square+4 square+….+nsquare….
S3=1 cube+2 cube+3 cube+4 cube+n cube….+
S4-1 exponent 4+2 exponent 4+….+n exponent 4+….
I find S4 followS3 and Sa+1 follow Sa.
I proved Sa=1exponent a+2 exponent a+3 exponent a+4 exponent a+….+n exponent a….
With a and n are two any number belong the sets of number.
problem eight.
for series of number with exponent n
1exponent n….2 exponent n….3 exponent n….4 exponent n….
second seriesof number with :2 exponent n-1 exponent n….3 exponent n-2 exponent n….4 exponent n-3 exponent n….5 exponent n-4exponent n….
From second series of number get big number subtract small number.We have third series of number.
continue and continue the end is zero.
at third series of number four number is function of 3,4 and n.
at x series of number, y number is the function of x,y and n.
example:
1^4…2^4….3^4….4^4….5^4….6^4….7^4….
second series of number is:
15….65….175….
third series of number is:
50….110….
second number off third series of number is 110.110 is the function of 2,3 and 4.2 is second number.3 is third series of number.4 is exponent number.
The and is zero and before zero is the number equal 4!=1 multiply 2 multiply 3 multiply 4.4 is the exponent number.
I understand and conclusions:
Sn=1^n+2^n+3^n+4^n+5^n+….+a^n+….
Sn+1=1^n+1+2^n+1+3^n+1+4^n+1+….+a^n+1+….
ATTENTION:2^n+1 is 2 exponent n+!.
I find Sn+! is the function of Sn or IF WE KNOW Sn WE KNOW Sn+!.
BEGIN with S1= 1+2+3+4+5+6+7+…..+a..
we know S1 inferred..we know S2 from S1 and we know S3 from S2 continue weknow Sx from Sx_-1
inferred WE have the formula about the total of series of number exponent z.z is number belong sets of number
I find this when I try prove fermat formula I think have CONTACT HERE..
PROVE FERMAT AT EXPONENT 3 AND CONTINUE TO 4 AND CONTINUE TO 5 AND TO n .n IS ANY NUMBER WHICH BELONG SETS OF NUMBER
To prove if formula fermat is right with exponent n inferred formula fermat is right with exponent n+1.
.THE CONTACT IS HERE. YOU inference from my problem to fermat formula.
THANK YOU SO MUCH.
FAREWELL FOREVER MY FANTASY MATHMATICS.
AU REVOIR POUR TOUJOURS MON FANTASMES MATHÉMATIQUES.
THE MAGICAL MATHEMATICIAN.TRANTANCUONG
Google Logos are awesome. I just found this google doodle
thanks for opening the google doodle window to the life of Fermat-the mathematician.
Yet another sliver of education provided to us by an amazing company. Thank you for all the fine work, making this chunk-O-turf we live on a more civilized place, and fun with math!
google’s logos never fail to pleasingly surprise and this one will delight the coterie of numero afficianados!